セルゲル広場は、地上部分はラウンドアバウト(環状交差点)になっています。このため、自動車がスムーズに走行できるよう、丸っぽい形が適しています。 一方、地下部分はショッピングモールになっており、店舗の面積を広くするには、四角っぽい形が適しています。 この一見、相反する要求を実現するために、丸と四角の中間的な形であるスーパー楕円が適していると言えます。


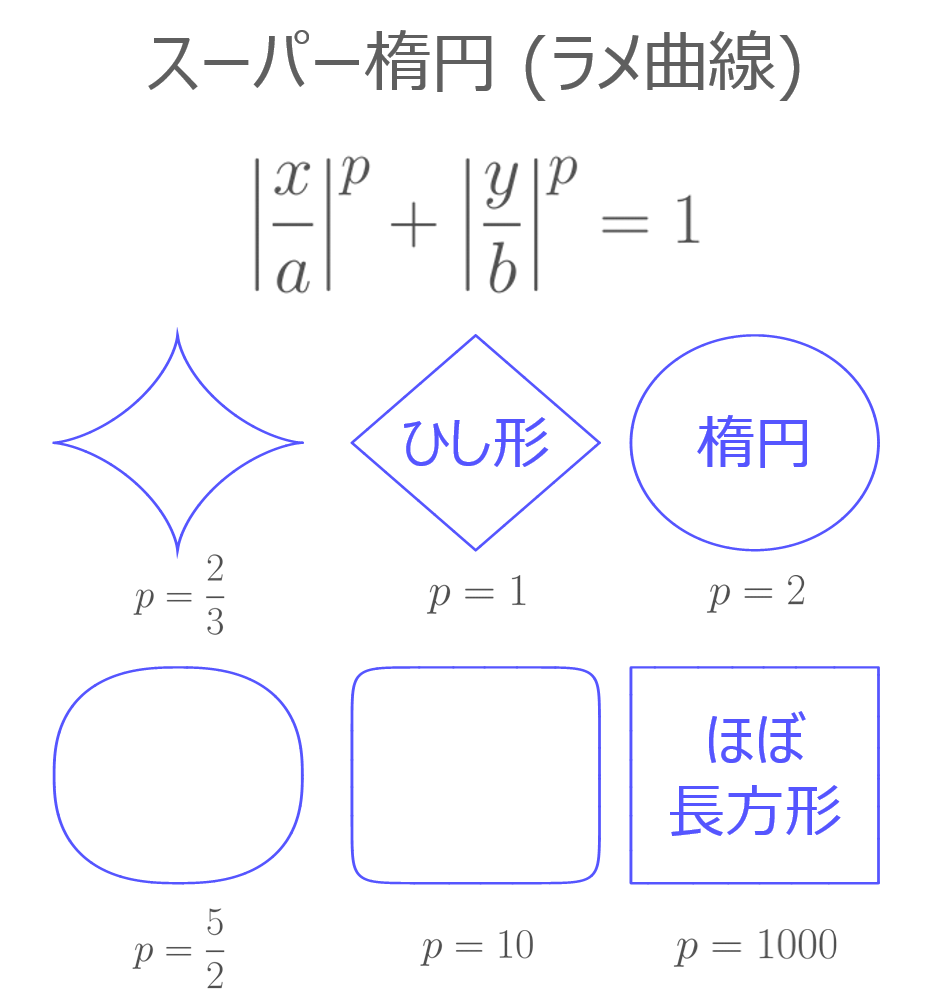

ラメ曲線やギーリス曲線に関係した画像です。










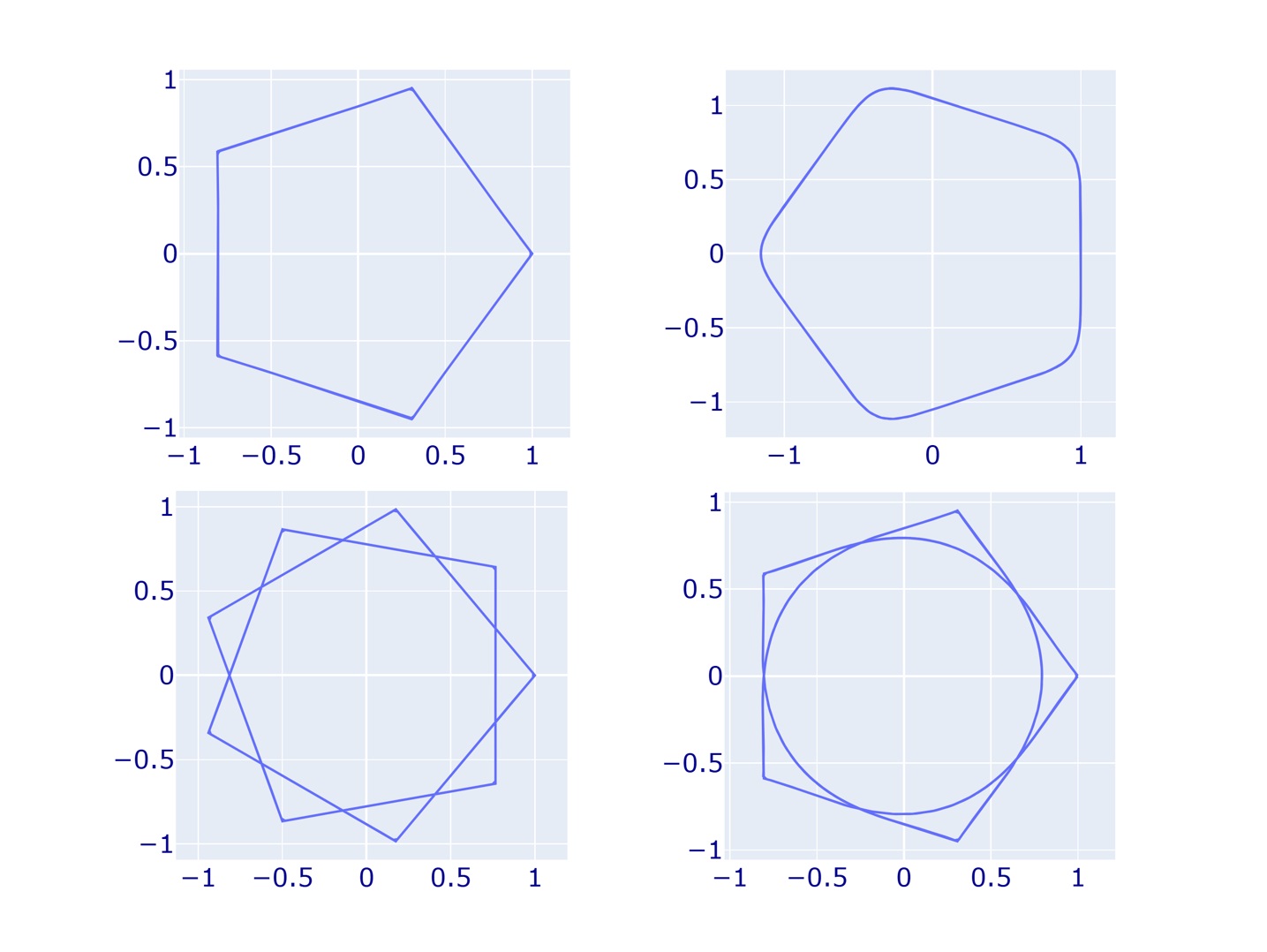
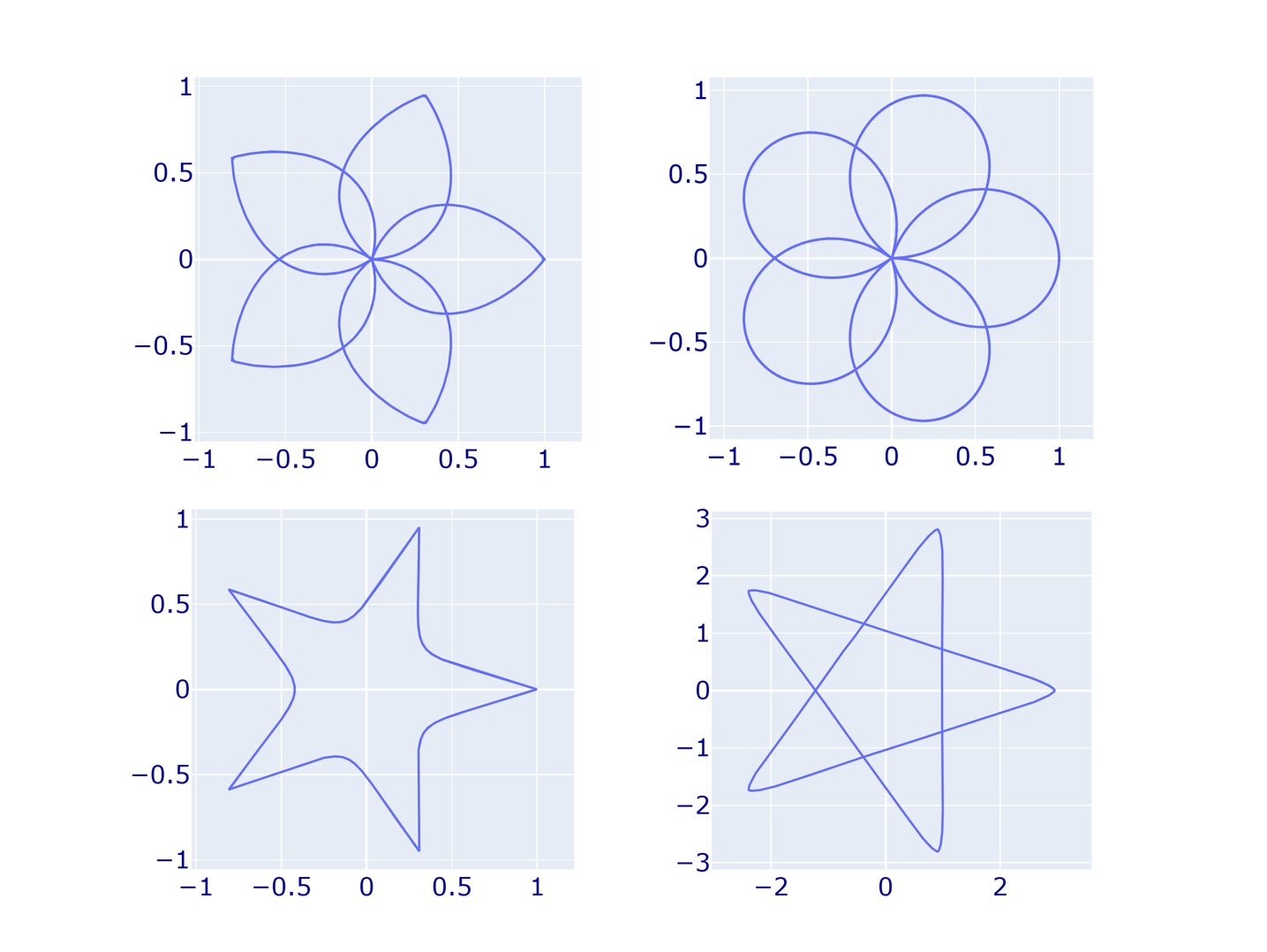
スーパー楕円やギーリス曲線に関する豆知識です。
セルゲル広場は、地上部分はラウンドアバウト(環状交差点)になっています。このため、自動車がスムーズに走行できるよう、丸っぽい形が適しています。 一方、地下部分はショッピングモールになっており、店舗の面積を広くするには、四角っぽい形が適しています。 この一見、相反する要求を実現するために、丸と四角の中間的な形であるスーパー楕円が適していると言えます。
機能性の観点から言えば、テーブルは四角い方が隅まで物が置けて便利です。 しかし、デザイン性の観点からは、四角いデーブルは堅い印象を与えがちで、オシャレで柔らかいイメージを演出するには、 丸っぽい方が適しています。このため、機能性とデザイン性を追求した結果、丸と四角の中間的な形であるスーパー楕円が採用されました。
東京ドームの屋根の外周は、スーパーサークル型(スーパー楕円の特殊なケースとして、縦横比が1:1の場合)です。 東京ドームの屋根は「ケーブル補強空気膜構造」という方式です。簡単に言えば、風船のように空気圧で膨らんでいますが、 それだけだと強度が十分ではないので、ケーブルで補強されています。 この構造において、境界にかかる 負荷を小さく抑えるためには、スーパーサークルが適していることから、この形状が採用されました。
スーパー楕円とラメ曲線は、基本的には同一の曲線です。 この曲線について初めて詳しく解析したのはフランス人の数学者ガブリエル・ラメです。 そのため、この曲線は数学の世界では、ラメ曲線として知られています。 一方、ピート・ハインがこの曲線をセルゲル広場のデザインに用いた際、スーパー楕円と呼んだため、 デザインの分野では、スーパー楕円という呼び名が広まりました。 なお、細かい呼び分けがされる場合もありますが、本サイトでは、特に断り書きのない限り、呼び分けはしていません。
スーパーフォーミュラとギーリス曲線は、基本的には同一の曲線です。 この曲線は、考案者のギーリス氏にちなんで、ギーリス曲線と呼ばれています。 一方、ギーリス氏自身は、おそらくスーパー楕円という呼称も意識して、自身の考案した 曲線(を表す方程式を)スーパーフォーミュラと読んでいます。 ただ、スーパーフォーミュラを直訳すると「すごい式」という感じで、漠然とした感じになるので、 このサイトでは、主としてギーリス曲線という呼称を用いることにします。
スーパー楕円の方程式は、比較的シンプルですが、数学的には適度な奥深さがあります。 特に、理学部や工学部において、数学の教材(各種理論の具体例)として適しています。 一例を挙げると、スーパー楕円に囲まれた部分の面積を求めると、「ガンマ関数」が出てきます。 ガンマ関数は、非負整数に対して定義される「階乗」の概念(例えば、「4の階乗」は4×3×2×1のこと、つまり24)を、 一般の実数の場合に拡張したものです。
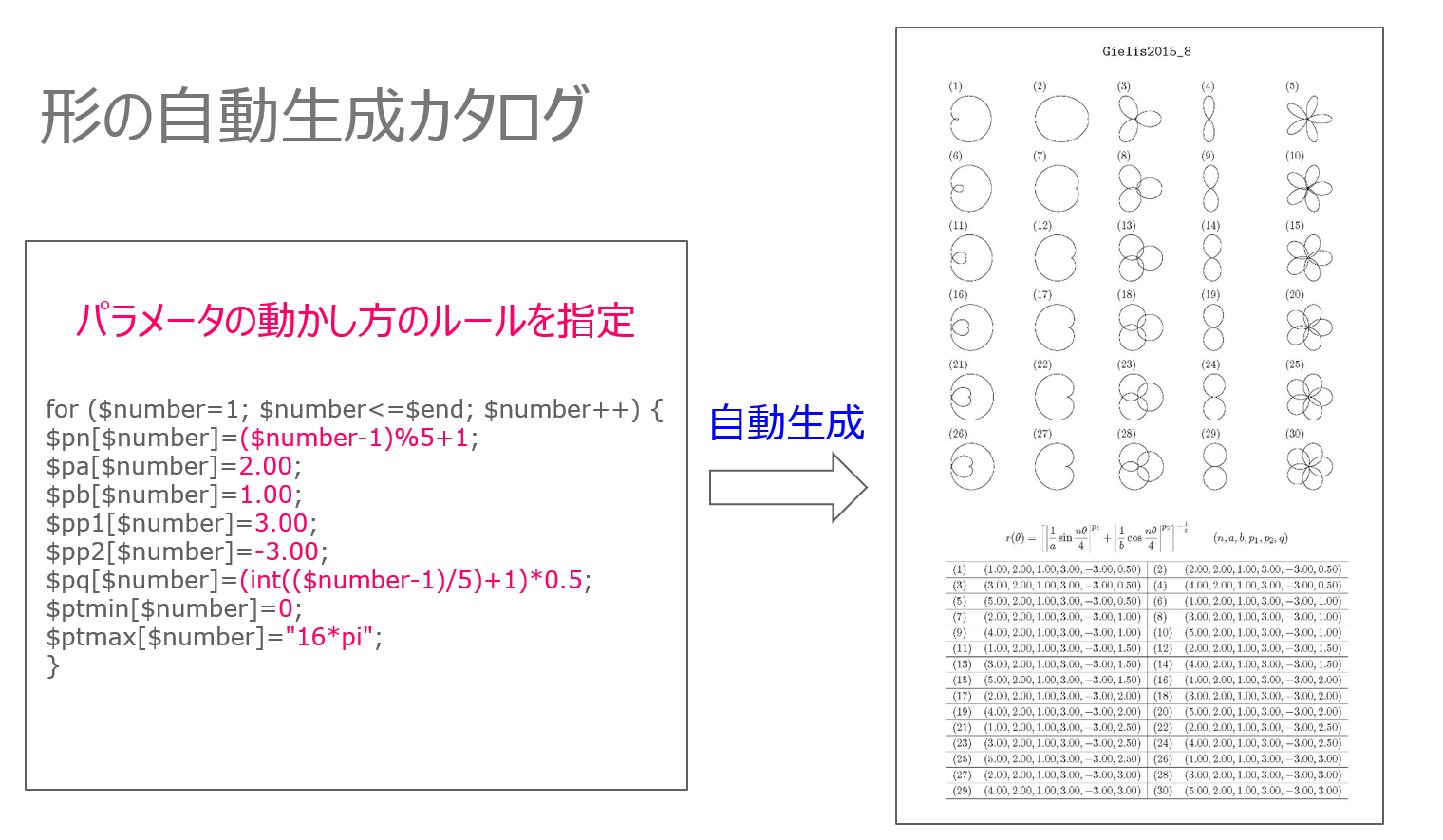
北欧デザインの数理(概要) intro.pdf
形のカタログの見本 catalog1.pdf
GeoGebra用スクリプト sample.ggb
※ファイルを開くには、GeoGebraをインストールするか、こちらのWebアプリを利用。